Protecting Data in Use: The Next Frontier for Data Security - Course Monster Blog
Over the last several years, significant progress has been achieved in protecting sensitive data in transit and storage. But sensitive data may still be vulnerable when it is in use. Consider the case of transparent database encryption (TDE). While TDE protects sensitive data in storage, the same data must be put in cleartext in the database buffer pool for SQL queries to be performed. This makes the sensitive data susceptible since its confidentiality might be compromised by memory-scraping malware or privileged user misuse, among other things.
Many firms have been hesitant to save money on IT infrastructure by outsourcing some calculations to the cloud and sharing private data with their peers for collaborative analytics because of concerns about data security. Two promising developing solutions for addressing this challenge and helping enterprises to realize the value of sensitive data are confidential computing and fully homomorphic encryption (FHE). What exactly are these things, and how do they differ?
Data in Use Protection Use Cases
Many businesses have struggled with sharing confidential data with collaborators and adopting cloud data services until recently. For some, the benefits of sharing data with collaborators and using cloud data services outweigh the danger of personal data becoming susceptible while in use. But, for other groups, such a trade-off is not on the table. What if companies were not required to make such a trade-off? What if data could be safeguarded not just during transmission and storage, but also during use? This would allow for a wide range of applications:
- Secure database processing for the cloud: To safeguard data as it travels between the database server and client apps, cloud database services use transport layer security (TLS). To secure data in storage, they use some database encryption approaches. When it comes to database query processing, however, the data must be stored in cleartext in the main memory. FHE may be used to query encrypted data directly, guaranteeing that sensitive information is encrypted in all three states: transport, storage, and usage. Confidential computing does not allow for query processing on encrypted data, but it may be used to ensure that such computations are carried out in a trusted execution environment (TEE), keeping sensitive data safe while in use.
- Secure data sharing for collaborative analytics: Organizations in the financial industry are required to exchange private data with their peers to assist avoid financial fraud. Organizations in the healthcare business must exchange private data to treat patients and research remedies for new ailments. In such situations, businesses must figure out how to get the intended result from exchanging private data while also adhering to data privacy standards. FHE can help solve this problem by running analytics directly on encrypted data, guaranteeing that the data is kept safe while in use. Confidential computing may be utilized to ensure that the data is integrated and processed within the TEE so that it is safeguarded while in use.
- Saving IT costs by delegating computation to the cloud: To better understand their consumers and personalize unique products for them, financial institutions build and deploy machine learning (ML) models. The marketing department, for example, could want to know if a client is likely to take out a loan in the next three months and customize an offer to them. Financial organizations may wish to reduce storage expenses by transferring customer data to a less expensive cloud storage service and doing analytics there. However, this raises concerns about the privacy of both the clients’ data and the ML models themselves. By encrypting the ML models and executing them directly on encrypted data, FHE can overcome this issue, guaranteeing that both the private data and the ML models are safe while in use. Confidential computing ensures that sensitive data and machine learning models are protected while in use by guaranteeing that the computation is performed within a TEE.
- Strengthening adherence to zero trust security principles: As common protective techniques such as TLS and TDE defeat assaults on data in transit and storage, attackers are turning their attention to data in use. In this context, attack techniques such as memory scraping, hypervisor and container breakout, and firmware compromise are used to target data in use. By eliminating the implicit confidence that applications would normally have to place in the underlying software stack to secure data in use, FHE and confidential computing help to increase adherence to zero trust security standards.
Confidential Computing
Because sensitive data is often stored in cleartext in the main memory, it may be susceptible during processing. Confidential computing tackles this issue by guaranteeing that sensitive data computations are done in a TEE, which is a hardware-based system that prohibits unauthorized access or change of sensitive data.
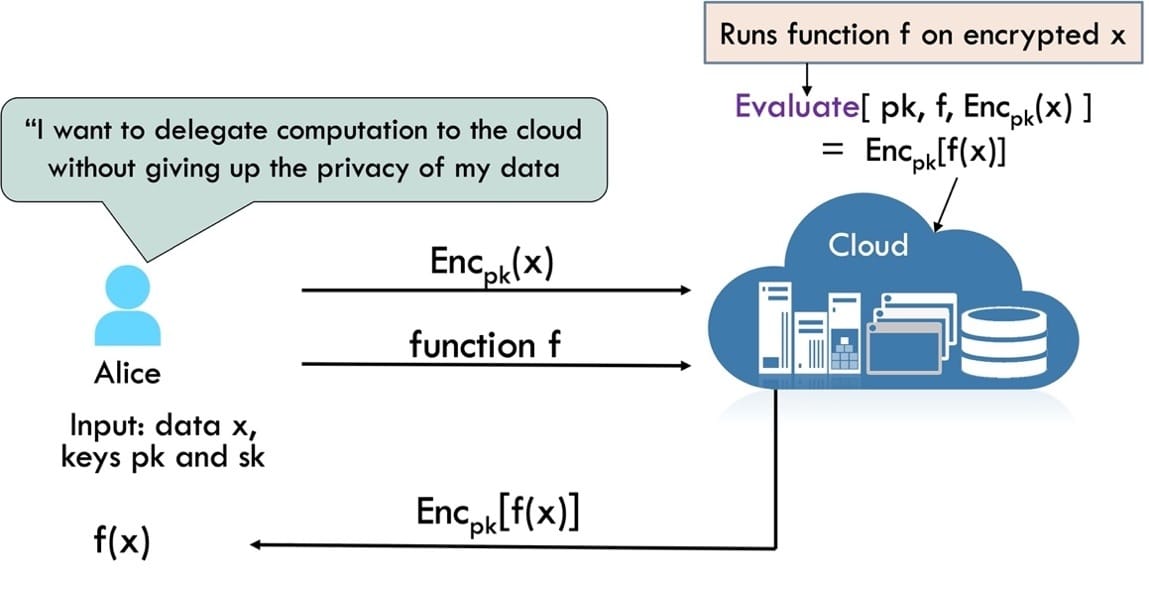
Figure 1: Protecting Sensitive Data During Computation Using Secure Enclaves.
One well-known example of secret computing is Intel Software Guard Extensions (SGX). It enables an application to construct a private portion of main memory, termed a secure enclave, whose content cannot be read or written by any process from outside the enclave regardless of its privilege level or central processing unit (CPU) mode. Even if the operating system (OS), hypervisor, or container engine are all hacked, the enclave is protected by this isolation. Furthermore, the enclave memory is encrypted using keys stored in the CPU. Only code within the enclave is decrypted inside the CPU. This means that a malevolent entity would be useless if they managed to physically take the enclave memory.
Two Approaches to Confidential Computing
For confidential computing, there are two primary options today: application software development kits (SDKs) and runtime deployment systems. The Intel SGX capability mentioned above is one example of the application SDK-based approach. The developer is in charge of partitioning the program into untrusted and trustworthy code in this technique. The OS executes the untrusted code normally, while the secure enclave runs the trustworthy code. The SDKs give you the tools you need to build and manage secure enclaves.
Another example of an application SDK-based solution is the Open Enclave SDK. It’s an open-source SDK that adds a layer of abstraction to TEE-based programs, allowing developers to create them once and distribute them across numerous hardware platforms. Because there is less code to analyze, the application SDK-based method provides for easier analysis of the trusted code, although it does need application modifications.
The purpose of the runtime deployment system-based method is to enable apps to operate in a TEE without having to rebuild them for a particular hardware platform or SDK. IBM Secure Execution for Linux (IBM Z15 and LinuxOne III) and the open-source project Enarx are two examples of solutions in this category. The runtime deployment system-based method has two major advantages: cost savings and faster time to value. However, deploying apps without making any changes may prohibit them from making use of other capabilities, such as attestation, unless they have been developed specifically for this purpose.
Fully Homomorphic Encryption
Traditional encryption systems, such as the advanced encryption standard (AES), may be relied upon to safeguard data in transit and storage. They do not, however, allow for calculation on encrypted data. To put it another way, data must first be encrypted before it can be used. Sensitive data might be exposed in this ‘data in use’ condition. FHE solves this problem by allowing computation on encrypted data directly. So, what precisely is homomorphic encryption, and what comprises a completely homomorphic encryption scheme?
A homomorphic encryption technique enables some type of computation on encrypted data. For example, given a cleartext input x and its encrypted value E(x), computing E(f(x)) for some function f should be doable without having access to x or any other secret information. Many well-known encryption methods display homomorphic features in this situation. A cleartext input x, for example, is encrypted as E(x) = xe mod m using RSA, where e is a public exponent and m is a public modulus. It is simple to see that, given two ciphertexts E(x) = xe mod m and E(y) = ye mod m, encrypting two cleartext inputs x and y, we can add them together and obtain (XY)e mod m, which is the encrypted value of XY. This means that RSA is homomorphic for multiplication.
Take, for example, the Paillier encryption technique. A cleartext input x is encrypted using Paillier as E(x) = gx rm mod m2, where g is the base, m is the modulus, and r is the random number. Given two ciphertexts E(x) = gx rm mod m2 and E(y) = gy sm mod m2, which encrypt two cleartext inputs x and y, we can easily multiply them together to produce g(x+y) (rs)m mod m2, which is the encrypted value of x + y. Paillier is homomorphic for addition in this sense. A homomorphic encryption scheme that allows just multiplication or only addition is called a partly homomorphic encryption scheme.
Early Attempts at Homomorphic Encryption
The number of operations that could be performed on encrypted data was limited in early systems that supported both multiplication and addition, such as DGHV. As a result, they’re known as relatively homomorphic encryption. For security reasons, a ‘noise’ is added during encryption in some systems.
This noise appears to increase with each addition or multiplication operation. This noise can accumulate to the point that the ciphertext cannot be decoded correctly. As a result, FHE refers to any technique that allows for an infinite amount of multiplications and adds on encrypted data.
Craig Gentry of IBM made the breakthrough in 2009. The first conceivable FHE scheme was his lattice-based encryption technique. The critical idea in Gentry’s work is called bootstrapping. Bootstrapping is the process of refreshing a ciphertext to create a new ciphertext that encrypts the same data but with less noise, allowing for more homomorphic operations to be evaluated on it.
Bootstrapping
Bootstrapping is the process of decrypting the ciphertext using the secret key and then re-encrypting the data. The secret key, on the other hand, is unknown. It is replaced with an encryption of the secret key, termed the bootstrapping key. Most FHE systems that have been discovered so far are based on bootstrapping.
Figure 2 shows how FHE may be utilized to delegate sensitive data processing to the cloud while keeping complete control over data privacy.
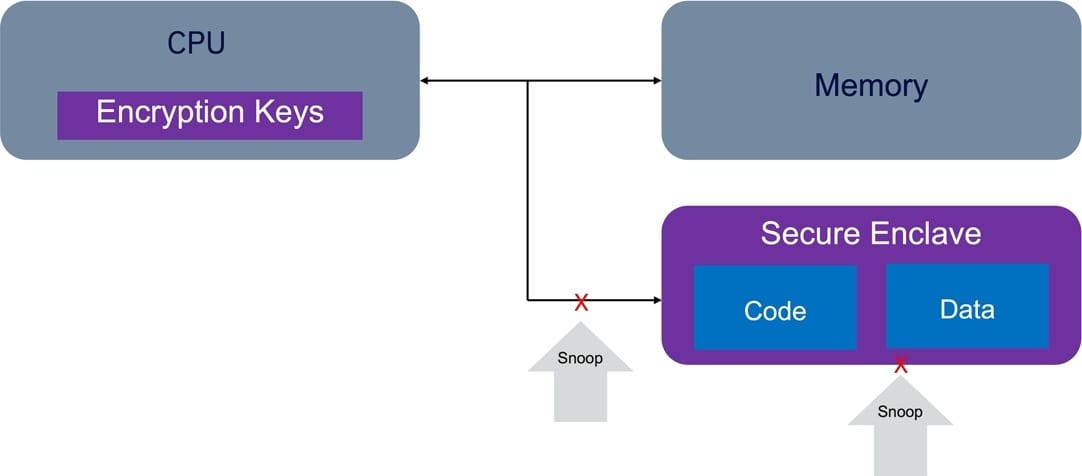
Figure 2: Fully Homomorphic Encryption.
FHE is an asymmetric encryption method, which necessitates the usage of a public key (pk) and a secret key (sk), as seen in the diagram. Alice uses the secret key sk to encrypt her data and provides her public key pk with the cloud service, which is used to evaluate function f on the encrypted data. When Alice receives the result, she decrypts it with her secret key and obtains f (x).
How Do FHE Schemes Work?
Depending on how they describe computing, FHE systems may be split into three categories:
- Boolean Circuits: This is best for number comparisons since it expresses computation as Boolean circuits. GSW and TFHE are two examples of such systems.
- Modular Arithmetic: This is best for integer arithmetic and scalar multiplication since it expresses computation as integer arithmetic. BGV and BFV are two examples of such systems.
- Approximate Arithmetic: This is best for polynomial approximations and ML models since it expresses computation as floating-point arithmetic. CKKS is one example of such a system.
There are several open-source FHE implementations available now. IBM HELib, PALISADE, and Microsoft SEAL are three of them; certain schemes, like CKKS, are accessible in all three libraries, while others aren’t. BGV, for instance, is only accessible in IBM HELib and PALISADE.
Comparing FHE and Confidential Computing
Both FHE and confidential computing are new technologies that help safeguard data in use. They assist in maintaining the privacy of sensitive/private data while it is in use. Because FHE is based on cryptography, its security can be mathematically proven. Confidential computing, on the other hand, is built on TEE. As a result, its safety cannot be mathematically proven. TEE, for example, can give a high level of security due to hardware-based isolation, but it can’t defend against side-channel attacks.
While FHE gives higher privacy assurances, it cannot provide code execution fidelity. This is where confidential computing excels. Confidential computing provides higher assurances for the integrity of code execution by executing programs within a TEE. As a result, FHE and secret computing should be seen as complementary rather than competing solutions.
Here at CourseMonster, we know how hard it may be to find the right time and funds for training. We provide effective training programs that enable you to select the training option that best meets the demands of your company.
For more information, please get in touch with one of our course advisers today or contact us at training@coursemonster.com




Comments ()